Lösen quadratischer Gleichungen

Die Methoden, um quadratische Gleichungen zu lösen, sind dieselben Methoden, um Nullstellen quadratischer Funktionen bzw. deren Graphen zu bestimmen. Anhand einiger Beispiele soll das hier erläutert werden.

Beispiel 1: Nullstellen von quadratischen Funktionsgraphen

Die allgemeine Form quadratischer Funktionen lautet: $f(x)= a x^2 + b x + c$
Für die Bestimmung von Nullstellen wird $f(x) = 0$ gesetzt. Für eine Beispielfunktion $f(x) = 2 x^2 + x - 4$ führt das zu \begin{align} 2 x^2 + x - 4 &= 0 \qquad \qquad \vert :2 \\ \\ x^2 + \frac{1}{2} x - \frac{4}{2} &= 0 \\ \\ x^2 + \frac{1}{2} x - 2 &= 0 \qquad \qquad \vert \frac{1}{2} = p ;\quad -2 = q \\ \\ x_{1,2} &= - \frac{\frac{1}{2}}{2} \pm \sqrt{ \left(\frac{\frac{1}{2}}{2} \right)^2 - \left(-2\right)} \\ \\ x_{1,2} &= - \frac{1}{4} \pm \sqrt{\left(\frac{1}{4}\right)^2 + 2} \\ \\ x_{1,2} &= - \frac{1}{4} \pm \sqrt{\frac{1}{16} + \frac{32}{16}} \\ \\ x_{1,2} &= - \frac{1}{4} \pm \sqrt{\frac{33}{16}} \\ \\ x_{1,2} &= - 0,25 \pm 1,436 \\ \\ x_1 = -1,686 \;&;\; x_2 = 1,186 \end{align}

Beispiel 2: Quadratische Funktionen nehmen einen bestimmten Funktionswert an

Hier gilt z.b.: $f(x) = -1$
Damit folgt: \begin{align} 2 x^2 + x - 4 &= -1 \qquad \qquad \vert +1 \\ \\ 2 x^2 + x - 3 &= 0 \qquad \qquad \vert :2 \\ \\ x^2 + \frac{1}{2} x - \frac{3}{2} &= 0 \qquad \qquad \vert \frac{1}{2} = p ;\quad -\frac{3}{2} = q \\ \\ x_{1,2} &= - \frac{\frac{1}{2}}{2} \pm \sqrt{\left(\frac{\frac{1}{2}}{2}\right)^2 - \left(\frac{3}{2}\right)} \\ \\ x_{1,2} &= - \frac{1}{4} \pm \sqrt{\left(\frac{1}{4}\right)^2 + \frac{3}{2}} \\ \\ x_{1,2} &= - \frac{1}{4} \pm \sqrt{\frac{1}{16} + \frac{24}{16}} \\ \\ x_{1,2} &= - \frac{1}{4} \pm \sqrt{\frac{25}{16}} \\ \\ x_{1,2} &= - 0,25 \pm 1,25 \\ \\ x_1 = -1,5 \;&;\; x_2 = 1 \end{align}

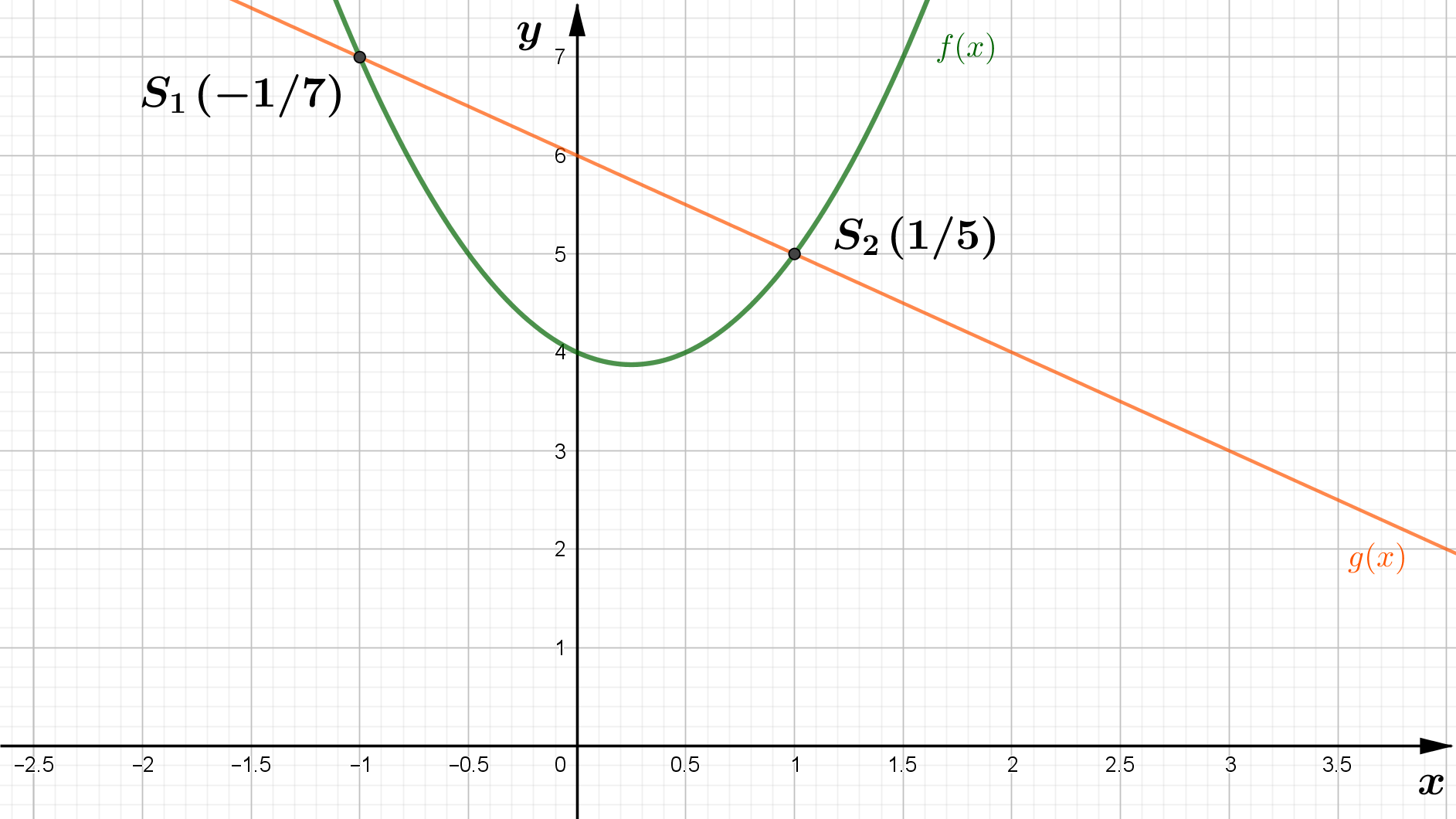
Beispiel 3: Quadratische Funktionsgraphen schneiden andere Graphen

Für die Schnittpunkte der beiden Funktionen f und g mit den Funktionstermen $$ f(x) = 2 x^2 - x + 4 \\ g(x) = -x + 6 $$ gilt der Ansatz $f(x) = g(x)$: \begin{align} 2 x^2 - x + 4 &= - x + 6 \qquad \qquad \vert +x \quad \vert - 6 \\ \\ 2 x^2 -2 &= 0 \qquad \qquad \vert +2 \\ \\ 2 x^2 &= 2 \qquad \qquad \vert : 2 \\ \\ x^2 &= 1 \qquad \qquad \vert \sqrt{(\ldots)} \\ \\ x_1 = -1 \;&;\; x_2 = 1 \end{align}